Fun,Think and discover!

1st solids-we know...
2nd-liquids-we know...
3rd-gasses-we know this too...
but...
did you know.....????

4th-plasma-in full detail......

In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas mayionize its molecules or atoms (reduce or increase the number of electrons in them), thus turning it into a plasma, which contains chargedparticles: positive ions and negative electrons or ions.^[1] Ionization can be induced by other means, such as strong electromagnetic field applied with a laser or microwave generator, and is accompanied by the dissociation of molecular bonds, if present.^[2]

The presence of a non-negligible number of charge carriers makes the plasma electrically conductive so that it responds strongly toelectromagnetic fields. Plasma, therefore, has properties quite unlike those of solids, liquids, or gases and is considered a distinct state of matter. Like gas, plasma does not have a definite shape or a definite volume unless enclosed in a container; unlike gas, under the influence of a magnetic field, it may form structures such as filaments, beams and double layer. Some common plasmas are stars and neon signs. In theuniverse, plasma is the most common state of matter for ordinary matter, most of which is in the rarefied intergalactic plasma (particularlyintracluster medium) and in stars.

Plasma properties and parameters

Artist's rendition of the Earth'splasma fountain, showing oxygen, helium, and hydrogen ions that gush into space from regions near the Earth's poles. The faint yellow area shown above the north pole represents gas lost from Earth into space; the green area is the aurora borealis, where plasma energy pours back into the atmosphere.^[5]

[edit]Definition of a plasma

Plasma is loosely described as an electrically neutral medium of positive and negative particles (i.e. the overall charge of a plasma is roughly zero). It is important to note that although they are unbound, these particles are not ‘free’. When the charges move they generate electrical currents with magnetic fields, and as a result, they are affected by each other’s fields. This governs their collective behavior with many degrees of freedom.^[2]^[6] A definition can have three criteria:^[7]^[8]

The plasma approximation: Charged particles must be close enough together that each particle influences many nearby charged particles, rather than just interacting with the closest particle (these collective effects are a distinguishing feature of a plasma). The plasma approximation is valid when the number of charge carriers within the sphere of influence (called the Debye sphere whose radius is the Debye screening length) of a particular particle is higher than unity to provide collective behavior of the charged particles. The average number of particles in the Debye sphere is given by the plasma parameter, "Λ" (the Greek letter Lambda).
Bulk interactions: The Debye screening length (defined above) is short compared to the physical size of the plasma. This criterion means that interactions in the bulk of the plasma are more important than those at its edges, where boundary effects may take place. When this criterion is satisfied, the plasma is quasineutral.
Plasma frequency: The electron plasma frequency (measuring plasma oscillations of the electrons) is large compared to the electron-neutral collision frequency (measuring frequency of collisions between electrons and neutral particles). When this condition is valid, electrostatic interactions dominate over

Ranges of plasma parameters

Plasma parameters can take on values varying by many orders of magnitude, but the properties of plasmas with apparently disparate parameters may be very similar (see plasma scaling). The following chart considers only conventional atomic plasmas and not exotic phenomena like quark gluon plasmas:

Range of plasmas. Density increases upwards, temperature increases towards the right. The free electrons in a metal may be considered an electron plasma.^[9]

Typical ranges of plasma parameters: orders of magnitude (OOM)
Characteristic	Terrestrial plasmas	Cosmic plasmas
Size in meters	10⁻⁶ m (lab plasmas) to 10² m (lightning) (~8 OOM)	10⁻⁶ m (spacecraft sheath) to 10²⁵ m (intergalactic nebula) (~31 OOM)
Lifetime in seconds	10⁻¹² s (laser-produced plasma) to 10⁷ s (fluorescent lights) (~19 OOM)	10¹ s (solar flares) to 10¹⁷ s (intergalactic plasma) (~16 OOM)
Density in particles per cubic meter	10⁷ m⁻³ to 10³² m⁻³ (inertial confinement plasma)	1 m⁻³ (intergalactic medium) to 10³⁰ m⁻³ (stellar core)
Temperature in kelvins	~0 K (crystalline non-neutral plasma^[10]) to 10⁸ K (magnetic fusion plasma)	10² K (aurora) to 10⁷ K (solar core)
Magnetic fields in teslas	10⁻⁴ T (lab plasma) to 10³ T (pulsed-power plasma)	10⁻¹² T (intergalactic medium) to 10¹¹ T (near neutron stars)

Degree of ionization

For plasma to exist, ionization is necessary. The term "plasma density" by itself usually refers to the "electron density", that is, the number of free electrons per unit volume. The degree of ionization of a plasma is the proportion of atoms that have lost (or gained) electrons, and is controlled mostly by the temperature. Even a partially ionized gas in which as little as 1% of the particles are ionized can have the characteristics of a plasma (i.e., response to magnetic fields and high electrical conductivity). The degree of ionization, α is defined as α = n_i/(n_i + n_a) where n_i is the number density of ions and n_ais the number density of neutral atoms. The electron density is related to this by the average charge state <Z> of the ions through n_e = <Z> n_i where n_eis the number density of electrons.

Potentials

Lightning is an example of plasma present at Earth's surface. Typically, lightning discharges 30,000 amperes at up to 100 million volts, and emits light, radio waves, X-rays and even gamma rays.^[12] Plasma temperatures in lightning can approach ~28,000 kelvin and electron densities may exceed 10²⁴ m⁻³.

Since plasmas are very good conductors, electric potentials play an important role. The potential as it exists on average in the space between charged particles, independent of the question of how it can be measured, is called the "plasma potential", or the "space potential". If an electrode is inserted into a plasma, its potential will generally lie considerably below the plasma potential due to what is termed a Debye sheath. The good electrical conductivity of plasmas makes their electric fields very small. This results in the important concept of "quasineutrality", which says the density of negative charges is approximately equal to the density of positive charges over large volumes of the plasma (n_e = <Z>n_i), but on the scale of the Debye length there can be charge imbalance. In the special case that double layers are formed, the charge separation can extend some tens of Debye lengths.

The magnitude of the potentials and electric fields must be determined by means other than simply finding the net charge density. A common example is to assume that the electrons satisfy the "Boltzmann relation":

$n_e \propto e^{e\Phi/k_BT_e}$ .

Differentiating this relation provides a means to calculate the electric field from the density:

$\vec{E} = (k_BT_e/e)(\nabla n_e/n_e)$ .

It is possible to produce a plasma that is not quasineutral. An electron beam, for example, has only negative charges. The density of a non-neutral plasma must generally be very low, or it must be very small, otherwise it will be dissipated by the repulsive electrostatic force.

In astrophysical plasmas, Debye screening prevents electric fields from directly affecting the plasma over large distances, i.e., greater than theDebye length. However, the existence of charged particles causes the plasma to generate and can be affected by magnetic fields. This can and does cause extremely complex behavior, such as the generation of plasma double layers, an object that separates charge over a few tens ofDebye lengths. The dynamics of plasmas interacting with external and self-generated magnetic fields are studied in the academic discipline ofmagnetohydrodynamics.

[edit]Magnetization

Plasma with a magnetic field strong enough to influence the motion of the charged particles is said to be magnetized. A common quantitative criterion is that a particle on average completes at least one gyration around the magnetic field before making a collision, i.e., ω_ce/ν_coll > 1, where ω_ce is the "electron gyrofrequency" and ν_coll is the "electron collision rate". It is often the case that the electrons are magnetized while the ions are not. Magnetized plasmas are anisotropic, meaning that their properties in the direction parallel to the magnetic field are different from those perpendicular to it. While electric fields in plasmas are usually small due to the high conductivity, the electric field associated with a plasma moving in a magnetic field is given by E = −v × B (where E is the electric field, v is the velocity, and B is the magnetic field), and is not affected by Debye shielding.^[13]

[edit]Comparison of plasma and gas phases

Plasma is often called the fourth state of matter. It is distinct from other lower-energy states of matter; most commonly solid, liquid, and gas. Although it is closely related to the gas phase in that it also has no definite form or volume, it differs in a number of ways, including the following:

Property	Gas	Plasma
Electrical conductivity	Very low: Air is an excellent insulator until it breaks down into plasma at electric field strengths above 30 kilovolts per centimeter.^[14]	Usually very high: For many purposes, the conductivity of a plasma may be treated as infinite.
Independently acting species	One: All gas particles behave in a similar way, influenced by gravity and by collisions with one another.	Two or three: Electrons, ions, protons and neutrons can be distinguished by the sign and value of their charge so that they behave independently in many circumstances, with different bulk velocities and temperatures, allowing phenomena such as new types of waves and instabilities.
Velocity distribution	Maxwellian: Collisions usually lead to a Maxwellian velocity distribution of all gas particles, with very few relatively fast particles.	Often non-Maxwellian: Collisional interactions are often weak in hot plasmas and external forcing can drive the plasma far from local equilibrium and lead to a significant population of unusually fast particles.
Interactions	Binary: Two-particle collisions are the rule, three-body collisions extremely rare.	Collective: Waves, or organized motion of plasma, are very important because the particles can interact at long ranges through the electric and magnetic forces.

[edit]Complex plasma phenomena

The remnant of "Tycho's Supernova", a huge ball of expanding plasma. The outer shell shown in blue is X-ray emission by high-speed electrons.

Although the underlying equations governing plasmas are relatively simple, plasma behavior is extraordinarily varied and subtle: the emergence of unexpected behavior from a simple model is a typical feature of a complex system. Such systems lie in some sense on the boundary between ordered and disordered behavior and cannot typically be described either by simple, smooth, mathematical functions, or by pure randomness. The spontaneous formation of interesting spatial features on a wide range of length scales is one manifestation of plasma complexity. The features are interesting, for example, because they are very sharp, spatially intermittent (the distance between features is much larger than the features themselves), or have a fractal form. Many of these features were first studied in the laboratory, and have subsequently been recognized throughout the universe. Examples of complexity and complex structures in plasmas include:

[edit]Filamentation

Striations or string-like structures^[15] are seen in many plasmas, like the plasma ball, the aurora,^[16] lightning,^[17] electric arcs, solar flares,^[18]and supernova remnants.^[19] They are sometimes associated with larger current densities, and the interaction with the magnetic field can form amagnetic rope structure.^[20] High power microwave breakdown at atmospheric pressure also leads to the formation of filamentary structures.^[21](See also Plasma pinch)

Filamentation also refers to the self-focusing of a high power laser pulse. At high powers, the nonlinear part of the index of refraction becomes important and causes a higher index of refraction in the center of the laser beam, where the laser is brighter than at the edges, causing a feedback that focuses the laser even more. The tighter focused laser has a higher peak brightness (irradiance) that forms a plasma. The plasma has an index of refraction lower than one, and causes a defocusing of the laser beam. The interplay of the focusing index of refraction, and the defocusing plasma makes the formation of a long filament of plasma that can be micrometers to kilometers in length.^[22] (See also Filament propagation)

[edit]Shocks or double layers

Plasma properties change rapidly (within a few Debye lengths) across a two-dimensional sheet in the presence of a (moving) shock or (stationary) double layer. Double layers involve localized charge separation, which causes a large potential difference across the layer, but does not generate an electric field outside the layer. Double layers separate adjacent plasma regions with different physical characteristics, and are often found in current carrying plasmas. They accelerate both ions and electrons.

[edit]Electric fields and circuits

Quasineutrality of a plasma requires that plasma currents close on themselves in electric circuits. Such circuits follow Kirchhoff's circuit laws and possess a resistance and inductance. These circuits must generally be treated as a strongly coupled system, with the behavior in each plasma region dependent on the entire circuit. It is this strong coupling between system elements, together with nonlinearity, which may lead to complex behavior. Electrical circuits in plasmas store inductive (magnetic) energy, and should the circuit be disrupted, for example, by a plasma instability, the inductive energy will be released as plasma heating and acceleration. This is a common explanation for the heating that takes place in the solar corona. Electric currents, and in particular, magnetic-field-aligned electric currents (which are sometimes generically referred to as "Birkeland currents"), are also observed in the Earth's aurora, and in plasma filaments.

[edit]Cellular structure

Narrow sheets with sharp gradients may separate regions with different properties such as magnetization, density and temperature, resulting in cell-like regions. Examples include the magnetosphere,heliosphere, and heliospheric current sheet. Hannes Alfvén wrote: "From the cosmological point of view, the most important new space research discovery is probably the cellular structure of space. As has been seen in every region of space accessible to in situ measurements, there are a number of 'cell walls', sheets of electric currents, which divide space into compartments with different magnetization, temperature, density, etc."^[23]

[edit]Critical ionization velocity

The critical ionization velocity is the relative velocity between an ionized plasma and a neutral gas, above which a runaway ionization process takes place. The critical ionization process is a quite general mechanism for the conversion of the kinetic energy of a rapidly streaming gas into ionization and plasma thermal energy. Critical phenomena in general are typical of complex systems, and may lead to sharp spatial or temporal features.

[edit]Ultracold plasma

Ultracold plasmas are created in a magneto-optical trap (MOT) by trapping and cooling neutral atoms, to temperatures of 1 mK or lower, and then using another laser to ionize the atoms by giving each of the outermost electrons just enough energy to escape the electrical attraction of its parent ion.

One advantage of ultracold plasmas are their well characterized and tunable initial conditions, including their size and electron temperature. By adjusting the wavelength of the ionizing laser, the kinetic energy of the liberated electrons can be tuned as low as 0.1 K, a limit set by the frequency bandwidth of the laser pulse. The ions inherit the millikelvin temperatures of the neutral atoms, but are quickly heated through a process known as disorder induced heating (DIH). This type of non-equilibrium ultracold plasma evolves rapidly, and displays many other interesting phenomena.^[24]

One of the metastable states of a strongly nonideal plasma is Rydberg matter, which forms upon condensation of excited atoms.

[edit]Non-neutral plasma

The strength and range of the electric force and the good conductivity of plasmas usually ensure that the densities of positive and negative charges in any sizeable region are equal ("quasineutrality"). A plasma with a significant excess of charge density, or, in the extreme case, is composed of a single species, is called a non-neutral plasma. In such a plasma, electric fields play a dominant role. Examples are charged particle beams, an electron cloud in a Penning trap and positron plasmas.^[25]

[edit]Dusty plasma and grain plasma

A dusty plasma contains tiny charged particles of dust (typically found in space), which also behave like a plasma. A plasma that contains larger particles is called grain plasma.

[edit]Mathematical descriptions

The complex self-constricting magnetic field lines and current paths in a field-aligned Birkeland currentthat can develop in a plasma.^[26]

Main article: Plasma modeling

To completely describe the state of a plasma, we would need to write down all the particle locations and velocities and describe the electromagnetic field in the plasma region. However, it is generally not practical or necessary to keep track of all the particles in a plasma. Therefore, plasma physicists commonly use less detailed descriptions, of which there are two main types:

[edit]Fluid model

Fluid models describe plasmas in terms of smoothed quantities, like density and averaged velocity around each position (see Plasma parameters). One simple fluid model, magnetohydrodynamics, treats the plasma as a single fluid governed by a combination of Maxwell's equations and the Navier–Stokes equations. A more general description is the two-fluid plasma picture, where the ions and electrons are described separately. Fluid models are often accurate when collisionality is sufficiently high to keep the plasma velocity distribution close to a Maxwell–Boltzmann distribution. Because fluid models usually describe the plasma in terms of a single flow at a certain temperature at each spatial location, they can neither capture velocity space structures like beams or double layers, nor resolve wave-particle effects.

[edit]Kinetic model

Kinetic models describe the particle velocity distribution function at each point in the plasma and therefore do not need to assume a Maxwell–Boltzmann distribution. A kinetic description is often necessary for collisionless plasmas. There are two common approaches to kinetic description of a plasma. One is based on representing the smoothed distribution function on a grid in velocity and position. The other, known as the particle-in-cell (PIC) technique, includes kinetic information by following the trajectories of a large number of individual particles. Kinetic models are generally more computationally intensive than fluid models. The Vlasov equation may be used to describe the dynamics of a system of charged particles interacting with an electromagnetic field. In magnetized plasmas, a gyrokinetic approach can substantially reduce the computational expense of a fully kinetic simulation.

[edit]Artificial plasmas

Most artificial plasmas are generated by the application of electric and/or magnetic fields. Plasma generated in a laboratory setting and for industrial use can be generally categorized by:

The type of power source used to generate the plasma—DC, RF and microwave
The pressure they operate at—vacuum pressure (< 10 mTorr or 1 Pa), moderate pressure (~ 1 Torr or 100 Pa), atmospheric pressure (760 Torr or 100 kPa)
The degree of ionization within the plasma—fully, partially, or weakly ionized
The temperature relationships within the plasma—thermal plasma (T_e = T_ion = T_gas), non-thermal or "cold" plasma (T_e >> T_ion = T_gas)
The electrode configuration used to generate the plasma
The magnetization of the particles within the plasma—magnetized (both ion and electrons are trapped in Larmor orbits by the magnetic field), partially magnetized (the electrons but not the ions are trapped by the magnetic field), non-magnetized (the magnetic field is too weak to trap the particles in orbits but may generate Lorentz forces)
The application

[edit]Generation of artificial plasma

Artificial plasma produced in air by aJacob's Ladder

Just like the many uses of plasma, there are several means for its generation, however, one principle is common to all of them: there must be energy input to produce and sustain it.^[27] For this case, plasma is generated when an electrical current is applied across a dielectric gas or fluid (an electrically non-conducting material) as can be seen in the image below, which shows a discharge tube as a simple example (DC used for simplicity).

Simple representation of a DC discharge tube.

Cascade process of ionization. Electrons are ‘e−’, neutral atoms ‘o’, and cations ‘+’.

The potential difference and subsequent electric field pull the bound electrons (negative) toward the anode (positive electrode) while the cathode (negative electrode) pulls the nucleus.^[28] As the voltage increases, the current stresses the material (by electric polarization) beyond its dielectric limit (termed strength) into a stage of electrical breakdown, marked by an electric spark, where the material transforms from being an insulator into a conductor (as it becomes increasingly ionized). This is a stage of avalanching ionization, where collisions between electrons and neutral gas atoms create more ions and electrons (as can be seen in the figure on the right). The first impact of an electron on an atom results in one ion and two electrons. Therefore, the number of charged particles increases rapidly (in the millions) only “after about 20 successive sets of collisions”,^[29] mainly due to a small mean free path (average distance travelled between collisions).

With ample current density and ionization, this forms a luminous electric arc (essentially lightning) between the electrodes.^{[Note 1]} Electrical resistance along the continuous electric arc creates heat, which ionizes more gas molecules (where degree of ionization is determined by temperature), and as per the sequence: solid-liquid-gas-plasma, the gas is gradually turned into a thermal plasma.^{[Note 2]} A thermal plasma is in thermal equilibrium, which is to say that the temperature is relatively homogeneous throughout the heavy particles (i.e. atoms, molecules and ions) and electrons. This is so because when thermal plasmas are generated, electrical energy is given to electrons, which, due to their great mobility and large numbers, are able to disperse it rapidly and byelastic collision (without energy loss) to the heavy particles.^[30]^{[Note 3]}

[edit]Examples of industrial/commercial plasma

Because of their sizable temperature and density ranges, plasmas find applications in many fields of research, technology and industry. For example, in: industrial and extractive metallurgy,^[30] surface treatments such as thermal spraying (coating), etching in microelectronics,^[31] metal cutting^[32] and welding; as well as in everyday vehicle exhaust cleanup and fluorescent/luminescent lamps,^[27] while even playing a part in supersonic combustion engines for aerospace engineering.^[33]

[edit]Low-pressure discharges

Glow discharge plasmas: non-thermal plasmas generated by the application of DC or low frequency RF (<100 kHz) electric field to the gap between two metal electrodes. Probably the most common plasma; this is the type of plasma generated within fluorescent light tubes.^[34]
Capacitively coupled plasma (CCP): similar to glow discharge plasmas, but generated with high frequency RF electric fields, typically 13.56 MHz. These differ from glow discharges in that the sheaths are much less intense. These are widely used in the microfabrication and integrated circuit manufacturing industries for plasma etching and plasma enhanced chemical vapor deposition.^[35]
Inductively coupled plasma (ICP): similar to a CCP and with similar applications but the electrode consists of a coil wrapped around the discharge volume that inductively excites the plasma.^{[citation needed]}
Wave heated plasma: similar to CCP and ICP in that it is typically RF (or microwave), but is heated by both electrostatic and electromagnetic means. Examples are helicon discharge, electron cyclotron resonance (ECR), and ion cyclotron resonance (ICR). These typically require a coaxial magnetic field for wave propagation.^{[citation needed]}

[edit]Atmospheric pressure

Arc discharge: this is a high power thermal discharge of very high temperature (~10,000 K). It can be generated using various power supplies. It is commonly used in metallurgical processes. For example, it is used to melt rocks containing Al₂O₃ to produce aluminium.
Corona discharge: this is a non-thermal discharge generated by the application of high voltage to sharp electrode tips. It is commonly used in ozone generators and particle precipitators.
Dielectric barrier discharge (DBD): this is a non-thermal discharge generated by the application of high voltages across small gaps wherein a non-conducting coating prevents the transition of the plasma discharge into an arc. It is often mislabeled 'Corona' discharge in industry and has similar application to corona discharges. It is also widely used in the web treatment of fabrics.^[36] The application of the discharge to synthetic fabrics and plastics functionalizes the surface and allows for paints, glues and similar materials to adhere.^[37]
Capacitive discharge: this is a nonthermal plasma generated by the application of RF power (e.g., 13.56 MHz) to one powered electrode, with a grounded electrode held at a small separation distance on the order of 1 cm. Such discharges are commonly stabilized using a noble gas such as helium or argon.^[38]

Temperatures

Einstein's argument

Consider a collection of N noninteracting particles, which can each be in one of two quantum states, $\scriptstyle|0\rangle$ and $\scriptstyle|1\rangle$ . If the two states are equal in energy, each different configuration is equally likely.

If we can tell which particle is which, there are

2 N

different configurations, since each particle can be in $\scriptstyle|0\rangle$ or $\scriptstyle|1\rangle$ independently. In almost all of the configurations, about half the particles are in $\scriptstyle|0\rangle$ and the other half in $\scriptstyle|1\rangle$ . The balance is a statistical effect: the number of configurations is largest when the particles are divided equally.

If the particles are indistinguishable, however, there are only N+1 different configurations. If there are K particles in state $\scriptstyle|1\rangle$ , there are N − K particles in state $\scriptstyle|0\rangle$ . Whether any particular particle is in state $\scriptstyle|0\rangle$ or in state $\scriptstyle|1\rangle$ cannot be determined, so each value of K determines a unique quantum state for the whole system. If all these states are equally likely, there is no statistical spreading out; it is just as likely for all the particles to sit in $\scriptstyle|0\rangle$ as for the particles to be split half and half.

Suppose now that the energy of state $\scriptstyle|1\rangle$ is slightly greater than the energy of state $\scriptstyle|0\rangle$ by an amount E. At temperature T, a particle will have a lesser probability to be in state $\scriptstyle|1\rangle$ by exp(−E/T). In the distinguishable case, the particle distribution will be biased slightly towards state $\scriptstyle|0\rangle$ and the distribution will be slightly different from half and half. But in the indistinguishable case, since there is no statistical pressure toward equal numbers, the most likely outcome is that most of the particles will collapse into state $\scriptstyle|0\rangle$ .

In the distinguishable case, for large N, the fraction in state $\scriptstyle|0\rangle$ can be computed. It is the same as flipping a coin with probability proportional to p = exp(−E/T) to land tails. The probability to land heads is 1/(1 + p), which is a smooth function of p, and thus of the energy.

In the indistinguishable case, each value of K is a single state, which has its own separate Boltzmann probability. So the probability distribution is exponential:

$\, P(K)= C e^{-KE/T} = C p^K.$

For large N, the normalization constant C is (1 − p). The expected total number of particles not in the lowest energy state, in the limit that $\scriptstyle N\rightarrow \infty$ , is equal to $\scriptstyle \sum_{n>0} C n p^n=p/(1-p)$ . It does not grow when N is large, it just approaches a constant. This will be a negligible fraction of the total number of particles. So a collection of enough Bose particles in thermal equilibrium will mostly be in the ground state, with only a few in any excited state, no matter how small the energy difference.

Consider now a gas of particles, which can be in different momentum states labeled $\scriptstyle|k\rangle$ . If the number of particles is less than the number of thermally accessible states, for high temperatures and low densities, the particles will all be in different states. In this limit the gas is classical. As the density increases or the temperature decreases, the number of accessible states per particle becomes smaller, and at some point more particles will be forced into a single state than the maximum allowed for that state by statistical weighting. From this point on, any extra particle added will go into the ground state.

To calculate the transition temperature at any density, integrate over all momentum states the expression for maximum number of excited particles p/(1 − p):

$\, N = V \int {d^3k \over (2\pi)^3} {p(k)\over 1-p(k)} = V \int {d^3k \over (2\pi)^3} {1 \over e^{k^2\over 2mT}-1}$

$\, p(k)= e^{-k^2\over 2mT}.$

When the integral is evaluated with the factors of k_B and ℏ restored by dimensional analysis, it gives the critical temperature formula of the preceding section. Therefore, this integral defines the critical temperature and particle number corresponding to the conditions of negligible chemical potential. In Bose–Einstein statistics distribution, μ is actually still nonzero for BEC's; however, μ is less than the ground state energy. Except when specifically talking about the ground state, μ can consequently be approximated for most energy or momentum states as μ ≈ 0.

[edit]Gross–Pitaevskii equation

Main article: Gross–Pitaevskii equation

The state of the BEC can be described by the wavefunction of the condensate $\psi(\vec{r})$ . For a system of this nature, $|\psi(\vec{r})|^2$ is interpreted as the particle density, so the total number of atoms is $N=\int d\vec{r}|\psi(\vec{r})|^2$

Provided essentially all atoms are in the condensate (that is, have condensed to the ground state), and treating the bosons using mean field theory, the energy (E) associated with the state $\psi(\vec{r})$ is:

$E=\int d\vec{r}\left[\frac{\hbar^2}{2m}|\nabla\psi(\vec{r})|^2+V(\vec{r})|\psi(\vec{r})|^2+\frac{1}{2}U_0|\psi(\vec{r})|^4\right]$

Minimizing this energy with respect to infinitesimal variations in $\psi(\vec{r})$ , and holding the number of atoms constant, yields the Gross-Pitaevski equation (GPE) (also a non-linear Schrödinger equation):

$i\hbar\frac{\partial \psi(\vec{r})}{\partial t} = \left(-\frac{\hbar^2\nabla^2}{2m}+V(\vec{r})+U_0|\psi(\vec{r})|^2\right)\psi(\vec{r})$

where:

$\,m$	is the mass of the bosons,
$\,V(\vec{r})$	is the external potential,
$\,U_0$	is representative of the inter-particle interactions.

The GPE provides a good description of the behavior of BEC's and is thus often applied for theoretical analysis.

[edit]Models beyond Gross–Pitaevskii

The Gross–Pitaevskii model of BEC is the physical approximation valid for certain classes of BEC's only. By construction, GPE uses the following simplifications: it assumes that interactions between condensate particles are of the contact two-body type and also it neglects anomalous contributions to self-energy.^[7] These assumptions are suitable mostly for the dilute three-dimensional condensates. If one relaxes any of these assumptions, the equation for the condensate wavefunction acquires the terms containing higher-order powers of the wavefunction. Moreover, for some physical systems the amount of such terms turns out to be infinite, therefore, the equation becomes essentially non-polynomial. The examples where this could happen are the Bose-Fermi composite condensates,^[8] effectively lower-dimensional condensates,^[9] and dense condensates and superfluid clusters and droplets.^[10]

[edit]Discovery

In 1938, Pyotr Kapitsa, John Allen and Don Misener discovered that helium-4 became a new kind of fluid, now known as a superfluid, at temperatures less than 2.17 K (the lambda point). Superfluid helium has many unusual properties, including zero viscosity (the ability to flow without dissipating energy) and the existence of quantized vortices. It was quickly realized that the superfluidity was due to partial Bose–Einstein condensation of the liquid. In fact, many of the properties of superfluid helium also appear in the gaseous Bose–Einstein condensates created by Cornell, Wieman and Ketterle (see below). Superfluid helium-4 is a liquid rather than a gas, which means that the interactions between the atoms are relatively strong; the original theory of Bose–Einstein condensation must be heavily modified in order to describe it. Bose–Einstein condensation remains, however, fundamental to the superfluid properties of helium-4. Note that helium-3, consisting of fermions instead of bosons, also enters a superfluid phase at low temperature, which can be explained by the formation of bosonic Cooper pairs of two atoms each (see also fermionic condensate).

The first "pure" Bose–Einstein condensate was created by Eric Cornell, Carl Wieman, and co-workers at JILA on June 5, 1995. They did this by cooling a dilute vapor consisting of approximately two thousand rubidium-87 atoms to below 170 nK using a combination of laser cooling (a technique that won its inventors Steven Chu, Claude Cohen-Tannoudji, and William D. Phillips the 1997 Nobel Prize in Physics) and magnetic evaporative cooling. About four months later, an independent effort led by Wolfgang Ketterle at MIT created a condensate made of sodium-23. Ketterle's condensate had about a hundred times more atoms, allowing him to obtain several important results such as the observation of quantum mechanical interference between two different condensates. Cornell, Wieman and Ketterle won the 2001 Nobel Prize in Physics for their achievements.^[11] A group led by Randall Hulet at Rice University announced the creation of a condensate of lithium atoms only one month following the JILA work.^[12] Lithium has attractive interactions which causes the condensate to be unstable and to collapse for all but a few atoms. Hulet and co-workers showed in a subsequent experiment that the condensate could be stabilized by the quantum pressure from trap confinement for up to about 1000 atoms.

The Bose–Einstein condensation also applies to quasiparticles in solids. A magnon in an antiferromagnet carries spin 1 and thus obeys Bose–Einstein statistics. The density of magnons is controlled by an external magnetic field, which plays the role of the magnon chemical potential. This technique provides access to a wide range of boson densities from the limit of a dilute Bose gas to that of a strongly interacting Bose liquid. A magnetic ordering observed at the point of condensation is the analog of superfluidity. In 1999 Bose condensation of magnons was demonstrated in the antiferromagnet Tl Cu Cl₃.^[13] The condensation was observed at temperatures as large as 14 K. Such a high transition temperature (relative to that of atomic gases) is due to the greater density achievable with magnons and the smaller mass (roughly equal to the mass of an electron). In 2006, condensation of magnons in ferromagnets was even shown at room temperature,^[14] where the authors used pumping techniques.

[edit]Velocity-distribution data graph

In the image accompanying this article, the velocity-distribution data indicates the formation of a Bose–Einstein condensate out of a gas of rubidium atoms. The false colors indicate the number of atoms at each velocity, with red being the fewest and white being the most. The areas appearing white and light blue are at the lowest velocities. The peak is not infinitely narrow because of theHeisenberg uncertainty principle: since the atoms are trapped in a particular region of space, their velocity distribution necessarily possesses a certain minimum width. This width is given by the curvature of the magnetic trapping potential in the given direction. More tightly confined directions have bigger widths in the ballistic velocity distribution. This anisotropy of the peak on the right is a purely quantum-mechanical effect and does not exist in the thermal distribution on the left. This famous graph served as the cover design for 1999 textbook Thermal Physics by Ralph Baierlein

[edit]Vortices

$\phi=\frac{nx}{\sqrt{2+x^2}}$ As in many other systems, vortices can exist in BECs. These can be created, for example, by 'stirring' the condensate with lasers, or rotating the confining trap. The vortex created will be a quantum vortex. These phenomena are allowed for by the non-linear $|\psi(\vec{r})|^2$ term in the GPE. As the vortices must have quantized angular momentum the wavefunction may have the form $\psi(\vec{r})=\phi(\rho,z)e^{i\ell\theta}$ where

ρ, z

and

θ

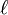are as in the cylindrical coordinate system, and $\ell$ is the angular number. This is particularly likely for an axially symmetric (for instance, harmonic) confining potential, which is commonly used. The notion is easily generalized. To determine

ϕ(ρ, z)

, the energy of $\psi(\vec{r})$ must be minimized, according to the constraint $\psi(\vec{r})=\phi(\rho,z)e^{i\ell\theta}$ . This is usually done computationally, however in a uniform medium the analytic form

where:

$\,n^2$	is	density far from the vortex,
$\,x = \frac{\rho}{\ell\xi},$
$\,\xi$	is	healing length of the condensate.

demonstrates the correct behavior, and is a good approximation.

A singly charged vortex ( $\ell=1$ ) is in the ground state, with its energy $\epsilon_v$ given by

$\epsilon_v=\pi n \frac{\hbar^2}{m}\ln\left(1.464\frac{b}{\xi}\right)$

where:

$\,b$

the farthest distance from the vortex considered.

(To obtain an energy which is well defined it is necessary to include this boundary

b

For multiply charged vortices ( $\ell >1$ ) the energy is approximated by

$\epsilon_v\approx \ell^2\pi n \frac{\hbar^2}{m}\ln\left(\frac{b}{\xi}\right)$

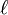which is greater than that of $\ell$ singly charged vortices, indicating that these multiply charged vortices are unstable to decay. Research has, however, indicated they are metastable states, so may have relatively long lifetimes.

Closely related to the creation of vortices in BECs is the generation of so-called dark solitons in one-dimensional BECs. These topological objects feature a phase gradient across their nodal plane, which stabilizes their shape even in propagation and interaction. Although solitons carry no charge and are thus prone to decay, relatively long-lived dark solitons have been produced and studied extensively.^[16]

[edit]Attractive interactions

The experiments led by Randall Hulet at Rice University from 1995 through 2000 showed that lithium condensates with attractive interactions could stably exist, but only up to a certain critical atom number. Beyond this critical number, the attraction overwhelmed the zero-point energy of the harmonic confining potential, causing the condensate to collapse in a burst reminiscent of a supernova explosion where an explosion is preceded by an implosion. By quench cooling the gas of lithium atoms, they observed the condensate to first grow, and subsequently collapse when the critical number was exceeded.

Further experimentation on attractive condensates was performed in 2000 by the JILA team, consisting of Cornell, Wieman, and coworkers. They originally used rubidium-87, an isotope whose atoms naturally repel each other, making a more stable condensate. Their instrumentation now had better control over the condensate so experimentation was made on naturally attracting atoms of another rubidium isotope, rubidium-85 (having negative atom-atom scattering length). Through a process called Feshbach resonance involving a sweep of the magnetic field causing spin flip collisions, they lowered the characteristic, discrete energies at which the rubidium atoms bond into molecules, making their Rb-85 atoms repulsive and creating a stable condensate. The reversible flip from attraction to repulsion stems from quantum interference among condensate atoms which behave as waves.

When the JILA team raised the magnetic field strength still further, the condensate suddenly reverted back to attraction, imploded and shrank beyond detection, and then exploded, expelling off about two-thirds of its 10,000 or so atoms. About half of the atoms in the condensate seemed to have disappeared from the experiment altogether, not being seen either in the cold remnant or the expanding gas cloud.^[11] Carl Wieman explained that under current atomic theory this characteristic of Bose–Einstein condensate could not be explained because the energy state of an atom near absolute zero should not be enough to cause an implosion; however, subsequent mean field theories have been proposed to explain it. The atoms that seem to have disappeared almost certainly still exist in some form, just not in a form that could be accounted for in that experiment. Most likely they formed molecules consisting of two bonded rubidium atoms^[17]. The energy gained by making this transition imparts a velocity sufficient for them to leave the trap without being detected.

[edit]Current research

Compared to more commonly encountered states of matter, Bose–Einstein condensates are extremely fragile. The slightest interaction with the outside world can be enough to warm them past the condensation threshold, eliminating their interesting properties and forming a normal gas.^{[citation needed]}

Nevertheless, they have proven useful in exploring a wide range of questions in fundamental physics, and the years since the initial discoveries by the JILA and MIT groups have seen an explosion in experimental and theoretical activity. Examples include experiments that have demonstrated interference between condensates due to wave-particle duality,^[18] the study of superfluidity and quantizedvortices, the creation of bright matter wave solitons from Bose condensates confined to one dimension, and the slowing of light pulses to very low speeds using electromagnetically induced transparency.^[19] Vortices in Bose–Einstein condensates are also currently the subject of analogue gravity research, studying the possibility of modeling black holes and their related phenomena in such environments in the lab. Experimentalists have also realized "optical lattices", where the interference pattern from overlapping lasers provides a periodic potential for the condensate. These have been used to explore the transition between a superfluid and a Mott insulator,^[20] and may be useful in studying Bose–Einstein condensation in fewer than three dimensions, for example the Tonks-Girardeau gas.

Bose–Einstein condensates composed of a wide range of isotopes have been produced.^[21]

Related experiments in cooling fermions rather than bosons to extremely low temperatures have created degenerate gases, where the atoms do not congregate in a single state due to the Pauli exclusion principle. To exhibit Bose–Einstein condensation, the fermions must "pair up" to form compound particles (e.g. molecules or Cooper pairs) that are bosons. The first molecular Bose–Einstein condensates were created in November 2003 by the groups of Rudolf Grimm at the University of Innsbruck, Deborah S. Jin at the University of Colorado at Boulder and Wolfgang Ketterle at MIT. Jin quickly went on to create the first fermionic condensate composed of Cooper pairs.^[22]

In 1999, Danish physicist Lene Vestergaard Hau led a team from Harvard University which succeeded in slowing a beam of light to about 17 metres per second^{[clarification needed]}. She was able to achieve this by using a superfluid.^[23] Hau and her associates at Harvard University have since successfully made a group of condensate atoms recoil from a "light pulse" such that they recorded the light's phase and amplitude, which was recovered by a second nearby condensate, by what they term "slow-light-mediated atomic matter-wave amplification" using Bose–Einstein condensates: details of the experiment are discussed in an article in the journal Nature, 8 February 2007.^[24]

Researchers in the new field of atomtronics use the properties of Bose–Einstein condensates when manipulating groups of identical cold atoms using lasers.

Isotopes

The spin-statistics theorem of Wolfgang Pauli states that half-integer spins (in units of $\scriptstyle \hbar$ ) lead to fermionic behaviour, e.g., the Pauli exclusion principle forbidding that more than two electrons possess the same energy, whereas integer spins lead to bosonic behaviour, e.g., condensation of identical bosonic particles in a common ground state.The effect has mainly been observed on alkaline atoms which have nuclear properties particularly suitable for working with traps. As of 2010, using ultra-low temperatures of 10^-7 K or below, Bose–Einstein condensates had been obtained for a multitude of isotopes, mainly of alkaline and alkaline earth atoms (⁷Li, ²³Na, ³⁹K, ⁴¹K, ⁸⁵Rb, ⁸⁷Rb, ¹³³Cs, ⁵²Cr, ⁴⁰Ca, ⁸⁴Sr, ⁸⁶Sr, ⁸⁸Sr, and ¹⁷⁴Yb). Condensation research was finally successful even with hydrogen with the aid of special methods. In contrast, the superfluid state of the bosonic ⁴He at temperatures below 2.17 K is not a good example of Bose–Einstein condensation, because the interaction between the ⁴He bosons is too strong. Only 8% of the atoms are in the single-particle ground state near zero temperature, rather than the 100% expected of a true Bose–Einstein condensate.

The bosonic, rather than fermionic, behaviour of some of these alkaline gases appears odd at first sight since their nuclei have half-integer total spin. The bosonic behaviour arises from a subtle interplay of electronic and nuclear spins: at ultra-low temperatures and corresponding excitation energies, the half-integer total spin of the electronic shell and the half-integer total spin of the nucleus of the atom are coupled by a very weak hyperfine interaction. The total spin of the atom arising from this coupling is an integer value leading to the bosonic ultra-low temperature behaviour of the atom. The chemistry of the systems at room temperature is determined by the electronic properties, which is essentially fermionic, since at room temperature thermal excitations have typical energies much higher than the hyperfine values.

$\,T_c$	is	the critical temperature,
$\,n$	is	the particle density,
$\,m$	is	the mass per boson,
$\hbar$	is	the reduced Planck constant,
$\,k_B$	is	the Boltzmann constant, and
$\,\zeta$	is	the Riemann zeta function; $\,\zeta(3/2)\approx 2.6124.$ (sequence A078434 in OEIS)

Fun,Think and discover!

Thursday, February 16, 2012

there are 5 states of matter!!!

Plasma properties and parameters

[edit]Definition of a plasma

Ranges of plasma parameters

Degree of ionization

Potentials

[edit]Magnetization

[edit]Comparison of plasma and gas phases

[edit]Complex plasma phenomena

[edit]Filamentation

[edit]Shocks or double layers

[edit]Electric fields and circuits

[edit]Cellular structure

[edit]Critical ionization velocity

[edit]Ultracold plasma

[edit]Non-neutral plasma

[edit]Dusty plasma and grain plasma

[edit]Mathematical descriptions

[edit]Fluid model

[edit]Kinetic model

[edit]Artificial plasmas

[edit]Generation of artificial plasma

[edit]Examples of industrial/commercial plasma

[edit]Low-pressure discharges

[edit]Atmospheric pressure

Temperatures

Einstein's argument

[edit]Gross–Pitaevskii equation

[edit]Models beyond Gross–Pitaevskii

[edit]Discovery

[edit]Velocity-distribution data graph

[edit]Vortices

[edit]Attractive interactions

[edit]Current research

Isotopes

Search my stuff